10296. Recursive function 1

Find the value of the function:

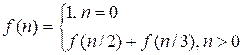
Input. One positive integer n (1 ≤ n ≤ 10¹⁸).

Output. Print the value of f(n).

Sample input	Sample output
5	5

SOLUTION

recursion - map

Algorithm analysis

Due to the limitation of n ≤ 10¹⁸, it is impossible to use a linear array to store the results of the function f. Therefore, we’ll use a map data structure.

Example

Consider the process of computing the function for n = 5:

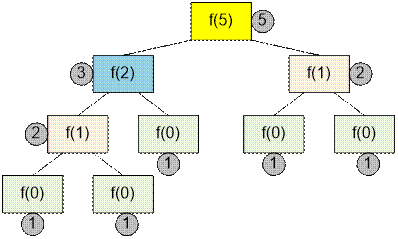
Algorithm realization

Declare a map m to store the function values: m[n] = f(n).

map<long long, long long> m;

Implement the function f.

long long f(long long n)

{

if (n == 0) return 1;

if (m.count(n) > 0) return m[n];

return m[n] = f(n / 2) + f(n / 3);

}

The main part of the program. Read the input value of n. Compute and print the value of the function f(n).

scanf("%lld", &n);

res = f(n);

printf("%lld\n", res);

Java realization

import java.util.*;

public class Main

{

static Map<Long, Long> m = new HashMap<Long, Long>();

static long n;

public static long f(long n)

{

if (m.containsKey(n)) return m.get(n);

if (n == 0) return 1;

long res = f(n/2) + f(n/3);

m.put(n,res);

return res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextLong();

System.out.println(f(n));

con.close();

}

}

Python realization

Declare a vocabulary m to store the function values: m[n] = f(n).

m = {}

Implement the function f.

def f(n):

if n == 0:

return 1

if n in m:

return m[n]

m[n] = f(n // 2) + f(n // 3)

return m[n]

The main part of the program. Read the input value of n. Compute and print the value of the function f(n).

n = int(input())

res = f(n)

print(res)